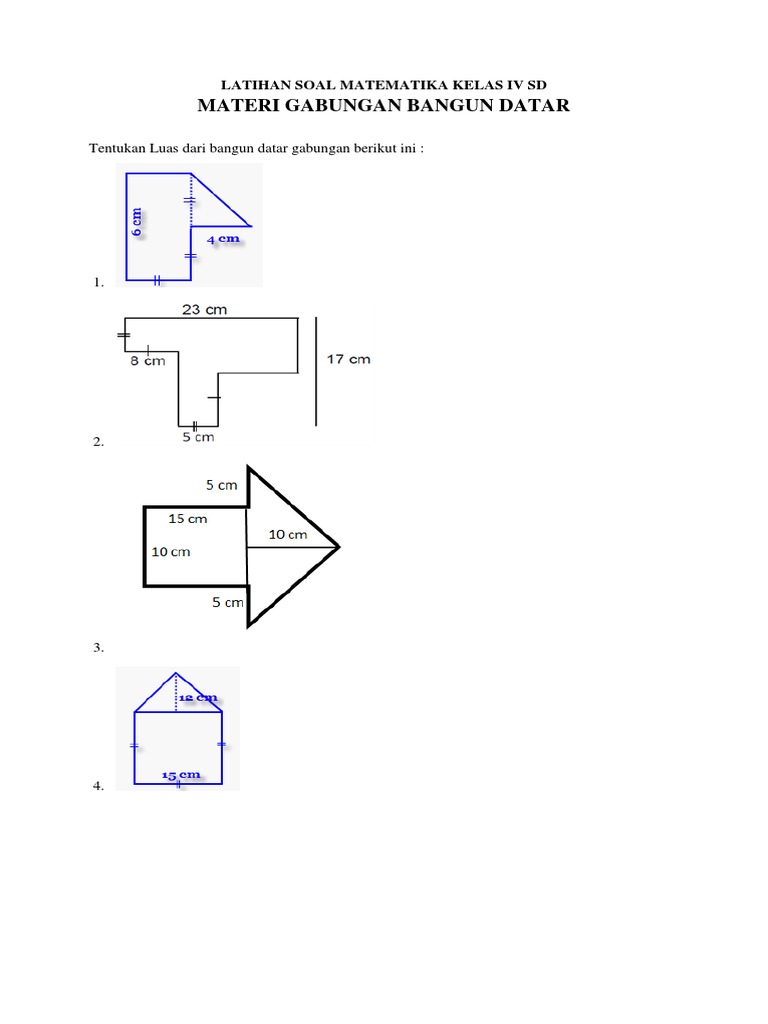
Menguasai Dunia Bentuk: Panduan Mendalam Soal Bangun Datar Matematika Kelas 4 Semester 2 Kurikulum 2013

Matematika, seringkali dianggap sebagai mata pelajaran yang menantang, sesungguhnya adalah fondasi penting dalam memahami dunia di sekitar kita. Khususnya bagi siswa kelas 4 Sekolah Dasar, pengenalan terhadap konsep bangun datar merupakan salah satu pilar utama dalam kurikulum matematika semester 2. Kurikulum 2013, dengan penekanannya pada pemahaman konseptual dan penerapan, menyajikan materi bangun datar melalui berbagai soal yang dirancang untuk mengasah kemampuan siswa dalam mengidentifikasi, mengukur, dan memanipulasi bentuk-bentuk geometris.

Artikel ini akan mengupas tuntas berbagai tipe soal bangun datar yang umum ditemui dalam pembelajaran matematika kelas 4 semester 2 kurikulum 2013. Kita akan membahas konsep-konsep dasar yang mendasarinya, strategi penyelesaian soal, serta memberikan contoh-contoh soal beserta pembahasannya yang mendalam. Tujuannya adalah agar para siswa, guru, maupun orang tua dapat memiliki pemahaman yang komprehensif dan strategi efektif dalam menghadapi materi ini.

Fondasi Konseptual: Mengenal Bangun Datar

Sebelum menyelami soal-soal, penting untuk kembali mengingat konsep dasar dari bangun datar itu sendiri. Bangun datar adalah bangun dua dimensi yang memiliki panjang dan lebar, tetapi tidak memiliki ketebalan atau tinggi. Beberapa bangun datar yang menjadi fokus utama di kelas 4 antara lain:

• Persegi: Bangun datar yang memiliki empat sisi sama panjang dan empat sudut siku-siku (90 derajat).
• Persegi Panjang: Bangun datar yang memiliki dua pasang sisi berhadapan sama panjang dan sejajar, serta empat sudut siku-siku.
• Segitiga: Bangun datar yang memiliki tiga sisi dan tiga sudut. Berdasarkan panjang sisinya, segitiga dapat dibedakan menjadi segitiga sama sisi, segitiga sama kaki, dan segitiga sembarang. Berdasarkan besar sudutnya, segitiga dapat dibedakan menjadi segitiga siku-siku, segitiga lancip, dan segitiga tumpul.
• Lingkaran: Bangun datar yang semua titik pada tepinya berjarak sama dari titik pusat.
• Jajar Genjang: Bangun datar yang memiliki dua pasang sisi berhadapan sama panjang dan sejajar. Sudut-sudutnya tidak selalu siku-siku.
• Trapesium: Bangun datar yang memiliki tepat sepasang sisi sejajar.

Selain identifikasi bangun datar, materi ini juga mencakup konsep-konsep penting seperti keliling (panjang garis tepi yang membatasi bangun datar) dan luas (besarnya area yang ditutupi oleh bangun datar).

Ragam Soal Bangun Datar Kelas 4 Semester 2 Kurikulum 2013

Kurikulum 2013 dirancang untuk mendorong siswa berpikir kritis dan menerapkan konsep. Oleh karena itu, soal-soal bangun datar tidak hanya sekadar menghafal rumus, melainkan lebih kepada pemahaman dan aplikasi. Berikut adalah beberapa tipe soal yang sering muncul:

1. Soal Identifikasi dan Sifat Bangun Datar

Tipe soal ini menguji pemahaman siswa tentang karakteristik setiap bangun datar.

• Contoh Soal: Bangun datar manakah yang memiliki empat sisi sama panjang dan keempat sudutnya siku-siku?

  • Pembahasan: Soal ini secara langsung menanyakan definisi dari sebuah bangun datar. Siswa perlu mengingat bahwa persegi adalah bangun datar yang memiliki ciri-ciri tersebut.

• Contoh Soal: Sebutkan minimal tiga perbedaan antara persegi dan persegi panjang.

  • Pembahasan: Ini adalah soal analisis yang meminta siswa untuk membandingkan dua bangun datar. Perbedaan utama meliputi panjang sisi (semua sisi sama pada persegi, sisi berhadapan sama pada persegi panjang) dan diagonal (sama panjang dan saling tegak lurus pada persegi, sama panjang pada persegi panjang).

2. Soal Menghitung Keliling Bangun Datar

Soal ini melibatkan penggunaan rumus keliling untuk menghitung panjang total garis tepi sebuah bangun datar.

• Rumus Dasar:

  • Keliling Persegi = 4 x sisi (s)
  • Keliling Persegi Panjang = 2 x (panjang (p) + lebar (l))
  • Keliling Segitiga = sisi a + sisi b + sisi c
  • Keliling Jajar Genjang = 2 x (sisi alas + sisi miring)
  • Keliling Trapesium = sisi alas + sisi atas + sisi miring 1 + sisi miring 2

• Contoh Soal: Sebuah taman berbentuk persegi panjang memiliki panjang 15 meter dan lebar 10 meter. Berapakah keliling taman tersebut?

  • Pembahasan:
    • Diketahui: p = 15 m, l = 10 m
    • Ditanya: Keliling taman
    • Rumus: Keliling = 2 x (p + l)
    • Perhitungan: Keliling = 2 x (15 m + 10 m) = 2 x 25 m = 50 meter.
    • Jadi, keliling taman tersebut adalah 50 meter.

• Contoh Soal: Sebuah lapangan berbentuk segitiga sama sisi memiliki panjang setiap sisinya 20 cm. Berapakah keliling lapangan tersebut?

  • Pembahasan:
    • Diketahui: sisi = 20 cm (karena segitiga sama sisi)
    • Ditanya: Keliling lapangan
    • Rumus: Keliling = sisi + sisi + sisi atau 3 x sisi
    • Perhitungan: Keliling = 20 cm + 20 cm + 20 cm = 60 cm.
    • Jadi, keliling lapangan tersebut adalah 60 cm.

3. Soal Menghitung Luas Bangun Datar

Soal ini melibatkan penggunaan rumus luas untuk menghitung area yang dicakup oleh sebuah bangun datar.

• Rumus Dasar:

  • Luas Persegi = sisi x sisi (s²)
  • Luas Persegi Panjang = panjang x lebar (p x l)
  • Luas Segitiga = ½ x alas x tinggi (½ x a x t)
  • Luas Jajar Genjang = alas x tinggi (a x t)
  • Luas Trapesium = ½ x (jumlah sisi sejajar) x tinggi (½ x (a+b) x t)

• Contoh Soal: Sebuah karpet berbentuk persegi memiliki panjang sisi 3 meter. Berapakah luas karpet tersebut?

  • Pembahasan:
    • Diketahui: sisi = 3 m
    • Ditanya: Luas karpet
    • Rumus: Luas = sisi x sisi
    • Perhitungan: Luas = 3 m x 3 m = 9 meter persegi.
    • Jadi, luas karpet tersebut adalah 9 meter persegi.

• Contoh Soal: Sebuah dinding kamar berbentuk persegi panjang dengan ukuran panjang 4 meter dan lebar 3 meter. Berapa luas dinding tersebut yang perlu dicat?

  • Pembahasan:
    • Diketahui: p = 4 m, l = 3 m
    • Ditanya: Luas dinding
    • Rumus: Luas = p x l
    • Perhitungan: Luas = 4 m x 3 m = 12 meter persegi.
    • Jadi, luas dinding yang perlu dicat adalah 12 meter persegi.

• Contoh Soal: Sebuah segitiga memiliki alas 10 cm dan tinggi 8 cm. Hitunglah luas segitiga tersebut.

  • Pembahasan:
    • Diketahui: alas = 10 cm, tinggi = 8 cm
    • Ditanya: Luas segitiga
    • Rumus: Luas = ½ x alas x tinggi
    • Perhitungan: Luas = ½ x 10 cm x 8 cm = ½ x 80 cm² = 40 cm².
    • Jadi, luas segitiga tersebut adalah 40 cm².

4. Soal Kombinasi Bangun Datar

Tipe soal ini seringkali lebih menantang karena melibatkan gabungan dari dua atau lebih bangun datar. Siswa perlu memecah bangun gabungan menjadi bangun-bangun sederhana untuk menghitung keliling atau luasnya.

• Contoh Soal: Perhatikan gambar berikut (bayangkan gambar sebuah rumah sederhana, di mana atapnya berbentuk segitiga dan badan rumahnya berbentuk persegi panjang). Jika panjang badan rumah adalah 8 meter, lebar badan rumah adalah 6 meter, dan tinggi segitiga atap adalah 3 meter, hitunglah luas total rumah tersebut (termasuk atap).

  • Pembahasan:
    • Bangun ini terdiri dari persegi panjang dan segitiga.
    • Luas Persegi Panjang (Badan Rumah):
      • Panjang = 8 m, Lebar = 6 m
      • Luas = p x l = 8 m x 6 m = 48 m²
    • Luas Segitiga (Atap):
      • Alas segitiga sama dengan lebar badan rumah = 6 m.
      • Tinggi segitiga = 3 m.
      • Luas = ½ x alas x tinggi = ½ x 6 m x 3 m = ½ x 18 m² = 9 m².
    • Luas Total: Luas Persegi Panjang + Luas Segitiga = 48 m² + 9 m² = 57 m².
    • Jadi, luas total rumah tersebut adalah 57 meter persegi.

• Contoh Soal: Sebuah lapangan berbentuk persegi panjang berukuran 20 meter x 15 meter. Di tengah lapangan terdapat kolam renang berbentuk lingkaran dengan diameter 7 meter. Berapakah luas area lapangan yang tidak ditutupi kolam renang?

  • Pembahasan:
    • Luas Lapangan Persegi Panjang:
      • Panjang = 20 m, Lebar = 15 m
      • Luas = p x l = 20 m x 15 m = 300 m².
    • Luas Kolam Renang Lingkaran:
      • Diameter = 7 m, maka jari-jari (r) = diameter / 2 = 7 m / 2 = 3.5 m.
      • Rumus Luas Lingkaran = π x r² (gunakan π ≈ 22/7 atau 3.14).
      • Luas = (22/7) x (3.5 m)² = (22/7) x 12.25 m² = 22 x 1.75 m² = 38.5 m².
    • Luas Area Lapangan yang Tidak Ditutupi Kolam Renang: Luas Lapangan – Luas Kolam Renang = 300 m² – 38.5 m² = 261.5 m².
    • Jadi, luas area lapangan yang tidak ditutupi kolam renang adalah 261.5 meter persegi.

5. Soal Aplikasi dalam Kehidupan Sehari-hari

Kurikulum 2013 sangat menekankan aplikasi matematika dalam kehidupan nyata. Soal-soal ini seringkali berbentuk cerita yang menggambarkan situasi praktis.

• Contoh Soal: Ibu ingin memasang keramik pada lantai dapur yang berukuran 4 meter x 3 meter. Jika setiap keramik berukuran 50 cm x 50 cm, berapa banyak keramik yang dibutuhkan?

  • Pembahasan:
    • Pertama, hitung luas lantai dapur.
      • Luas = 4 m x 3 m = 12 m².
    • Kedua, hitung luas satu keramik.
      • Ubah satuan ke meter: 50 cm = 0.5 meter.
      • Luas keramik = 0.5 m x 0.5 m = 0.25 m².
    • Ketiga, bagi luas lantai dengan luas satu keramik.
      • Jumlah keramik = Luas Lantai / Luas Keramik = 12 m² / 0.25 m² = 48 keramik.
    • Jadi, dibutuhkan 48 keramik untuk lantai dapur tersebut.

• Contoh Soal: Budi ingin membuat pagar di sekeliling kebunnya yang berbentuk persegi panjang dengan panjang 12 meter dan lebar 8 meter. Jika harga 1 meter pagar adalah Rp 50.000, berapa total biaya yang dibutuhkan Budi untuk membuat pagar?

  • Pembahasan:
    • Pertama, hitung keliling kebun.
      • Keliling = 2 x (panjang + lebar) = 2 x (12 m + 8 m) = 2 x 20 m = 40 meter.
    • Kedua, hitung total biaya.
      • Total Biaya = Keliling x Harga per meter = 40 meter x Rp 50.000/meter = Rp 2.000.000.
    • Jadi, total biaya yang dibutuhkan Budi untuk membuat pagar adalah Rp 2.000.000.

Strategi Jitu Menguasai Soal Bangun Datar

Untuk sukses dalam mengerjakan soal-soal bangun datar, siswa dapat menerapkan beberapa strategi berikut:

1. Pahami Konsep Dasar: Pastikan benar-benar mengerti definisi, sifat, dan perbedaan antara setiap bangun datar. Gunakan gambar dan alat peraga untuk memvisualisasikan.
2. Hafalkan Rumus dengan Benar: Rumus keliling dan luas adalah kunci. Tulis rumus-rumus ini di kartu atau tempel di tempat yang mudah dilihat. Latihan berulang kali akan membantu menghafalnya.
3. Baca Soal dengan Teliti: Pahami apa yang ditanyakan oleh soal. Identifikasi informasi yang diberikan (panjang, lebar, sisi, diameter, tinggi, dll.) dan apa yang diminta (keliling, luas, jumlah, biaya, dll.).
4. Gunakan Gambar: Jika soal tidak disertai gambar, buatlah sketsa sederhana dari bangun datar yang dimaksud. Ini sangat membantu, terutama untuk soal kombinasi bangun datar.
5. Perhatikan Satuan: Pastikan semua satuan yang digunakan dalam perhitungan adalah sama. Jika ada satuan yang berbeda (misalnya meter dan sentimeter), ubah salah satunya agar konsisten.
6. Pecah Soal Kompleks: Untuk soal kombinasi bangun datar, pecahlah menjadi bangun-bangun sederhana yang sudah dikenal. Hitung luas atau keliling masing-masing bagian, lalu gabungkan hasilnya sesuai instruksi soal.
7. Latihan Soal Bervariasi: Kerjakan berbagai macam soal, mulai dari yang paling mudah hingga yang menantang. Semakin banyak latihan, semakin terbiasa siswa dengan pola soal dan cara penyelesaiannya.
8. Diskusi dan Tanya: Jangan ragu untuk bertanya kepada guru atau teman jika ada materi yang belum dipahami. Berdiskusi dengan teman juga bisa membuka wawasan baru dalam mencari solusi.

Kesimpulan

Mempelajari bangun datar bukan sekadar menghafal rumus, melainkan mengembangkan kemampuan spasial, logika, dan pemecahan masalah. Soal-soal bangun datar dalam kurikulum 2013 kelas 4 semester 2 dirancang untuk menstimulasi pemikiran kritis dan menghubungkan konsep matematika dengan kehidupan sehari-hari. Dengan pemahaman konsep yang kuat, penguasaan rumus yang tepat, dan strategi penyelesaian yang efektif, siswa dapat menaklukkan setiap tantangan soal bangun datar dan membangun fondasi matematika yang kokoh untuk jenjang pendidikan selanjutnya. Mari jadikan belajar bangun datar sebagai petualangan yang menyenangkan dalam menjelajahi dunia bentuk dan ruang!