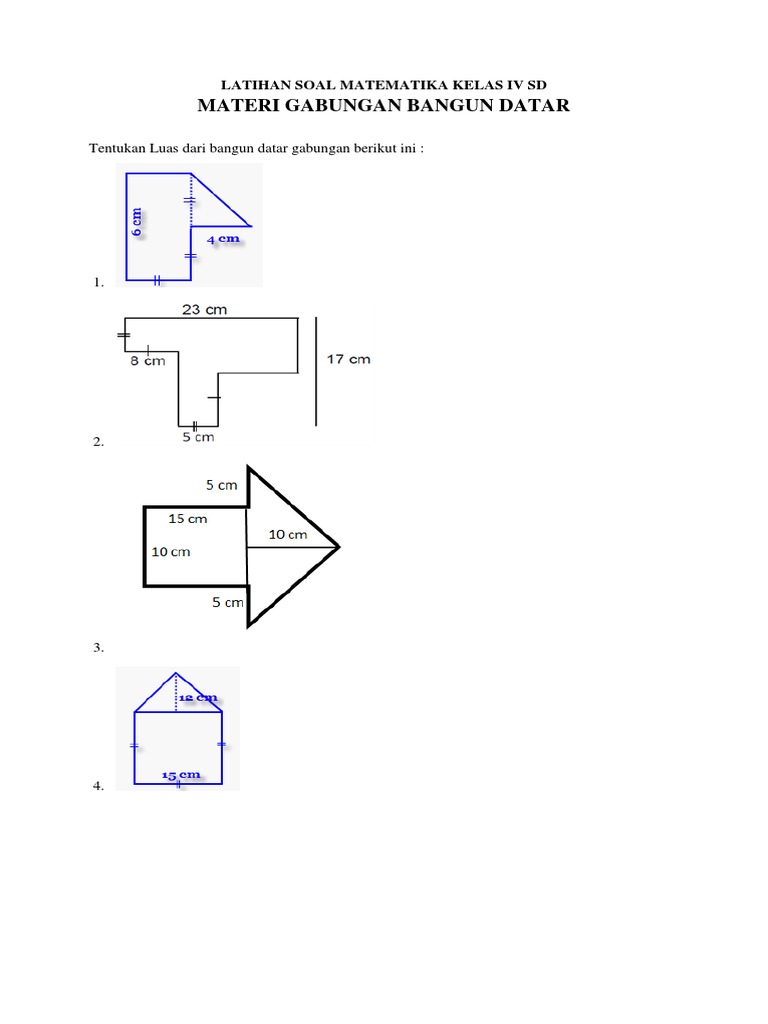
Menguasai Bangun Datar: Panduan Lengkap Soal Kelas 4 Semester 2
Memasuki semester kedua di kelas 4, siswa akan dihadapkan pada materi geometri yang lebih mendalam, khususnya mengenai bangun datar. Materi ini merupakan fondasi penting untuk pemahaman konsep matematika yang lebih kompleks di jenjang berikutnya. Semester 2 biasanya mencakup berbagai jenis bangun datar, sifat-sifatnya, serta perhitungan yang berkaitan dengan keliling dan luasnya.
Artikel ini akan menjadi panduan lengkap bagi siswa kelas 4, orang tua, dan pendidik dalam memahami berbagai jenis soal bangun datar yang umum diujikan pada semester 2. Kita akan membahas konsep-konsep kunci, strategi penyelesaian, serta contoh-contoh soal yang bervariasi.
1. Mengenal Kembali Bangun Datar Dasar
Sebelum melangkah lebih jauh, penting untuk merevitalisasi pemahaman siswa tentang bangun datar dasar yang telah dipelajari di semester sebelumnya. Bangun datar adalah bangun dua dimensi yang hanya memiliki panjang dan lebar, tanpa ketebalan.
- Persegi: Bangun datar dengan empat sisi yang sama panjang dan empat sudut siku-siku (90 derajat).
- Persegi Panjang: Bangun datar dengan dua pasang sisi yang berhadapan sama panjang dan empat sudut siku-siku.
- Segitiga: Bangun datar yang memiliki tiga sisi dan tiga sudut. Segitiga dapat diklasifikasikan berdasarkan panjang sisinya (segitiga sama sisi, sama kaki, sembarang) dan besar sudutnya (segitiga lancip, siku-siku, tumpul).
- Lingkaran: Bangun datar yang semua titik pada kelilingnya berjarak sama dari titik pusat.
2. Memperdalam Sifat-Sifat Bangun Datar
Semester 2 seringkali lebih menekankan pada pemahaman sifat-sifat masing-masing bangun datar secara lebih rinci. Siswa diharapkan mampu mengidentifikasi dan menjelaskan ciri-ciri unik dari setiap bangun.
-
Persegi:
- Memiliki 4 sisi sama panjang.
- Memiliki 4 sudut siku-siku.
- Memiliki 2 diagonal yang sama panjang dan saling berpotongan tegak lurus di titik pusat.
- Memiliki 4 sumbu simetri.
-
Persegi Panjang:
- Memiliki 2 pasang sisi berhadapan sama panjang.
- Memiliki 4 sudut siku-siku.
- Memiliki 2 diagonal yang sama panjang dan berpotongan di titik pusat.
- Memiliki 2 sumbu simetri.
-
Segitiga:
- Segitiga Sama Sisi: 3 sisi sama panjang, 3 sudut sama besar (masing-masing 60 derajat), 3 sumbu simetri.
- Segitiga Sama Kaki: 2 sisi sama panjang, 2 sudut alas sama besar, 1 sumbu simetri.
- Segitiga Siku-siku: Memiliki 1 sudut siku-siku (90 derajat).
- Segitiga Lancip: Semua sudut kurang dari 90 derajat.
- Segitiga Tumpul: Memiliki 1 sudut lebih dari 90 derajat.
-
Lingkaran:
- Memiliki titik pusat.
- Jari-jari (r): Jarak dari titik pusat ke setiap titik pada keliling.
- Diameter (d): Garis lurus yang melewati titik pusat dan menghubungkan dua titik pada keliling (d = 2r).
- Keliling: Jarak mengelilingi tepi lingkaran.
3. Keliling Bangun Datar: Mengukur Batas Luar
Salah satu konsep utama dalam bangun datar adalah keliling. Keliling adalah panjang total garis yang membentuk batas luar suatu bangun datar. Siswa kelas 4 semester 2 akan diuji kemampuannya dalam menghitung keliling berbagai bangun datar, baik yang sederhana maupun yang lebih kompleks.
-
Rumus Keliling Persegi:
Keliling = sisi + sisi + sisi + sisi = 4 × sisi
Contoh Soal: Sebuah taman berbentuk persegi memiliki panjang sisi 8 meter. Berapakah keliling taman tersebut?
Penyelesaian: Keliling = 4 × 8 meter = 32 meter. -
Rumus Keliling Persegi Panjang:
Keliling = panjang + lebar + panjang + lebar = 2 × (panjang + lebar)
Contoh Soal: Sebuah lapangan basket memiliki panjang 28 meter dan lebar 15 meter. Hitunglah keliling lapangan tersebut!
Penyelesaian: Keliling = 2 × (28 meter + 15 meter) = 2 × 43 meter = 86 meter. -
Rumus Keliling Segitiga:
Keliling = sisi a + sisi b + sisi c
Contoh Soal: Segitiga memiliki panjang sisi 7 cm, 9 cm, dan 12 cm. Berapakah keliling segitiga tersebut?
Penyelesaian: Keliling = 7 cm + 9 cm + 12 cm = 28 cm. -
Rumus Keliling Lingkaran:
Keliling = 2 × π × jari-jari (r)
atau
Keliling = π × diameter (d)
(Di mana π (pi) biasanya dibulatkan menjadi 3,14 atau 22/7)
Contoh Soal 1: Sebuah roda sepeda memiliki jari-jari 35 cm. Hitunglah keliling roda tersebut menggunakan π = 22/7!
Penyelesaian: Keliling = 2 × (22/7) × 35 cm = 2 × 22 × 5 cm = 220 cm.
Contoh Soal 2: Sebuah kolam renang berbentuk lingkaran memiliki diameter 14 meter. Hitunglah keliling kolam renang tersebut menggunakan π = 3,14!
Penyelesaian: Keliling = 3,14 × 14 meter = 43,96 meter. -
Soal Keliling Gabungan Bangun Datar:
Pada semester 2, siswa juga akan bertemu dengan soal-soal yang melibatkan gabungan dua atau lebih bangun datar. Untuk menyelesaikannya, siswa perlu mengidentifikasi bagian-bagian mana yang membentuk keliling total dan bagian mana yang berada di dalam.
Contoh Soal: Perhatikan gambar sebuah rumah (persegi panjang dengan atap segitiga di atasnya). Persegi panjang memiliki panjang 10 meter dan lebar 6 meter. Sisi alas segitiga sama dengan lebar persegi panjang. Jika sisi miring segitiga adalah 5 meter, berapakah keliling rumah tersebut (hanya bagian luar)?
Penyelesaian: Keliling = panjang persegi panjang + lebar persegi panjang + sisi miring segitiga + sisi miring segitiga.
(Perhatikan bahwa alas segitiga tidak termasuk dalam keliling luar karena berada di dalam).
Keliling = 10 m + 6 m + 5 m + 5 m = 26 meter.
4. Luas Bangun Datar: Mengukur Besarnya Permukaan
Selain keliling, luas adalah konsep penting lainnya yang dipelajari. Luas mengukur seberapa besar permukaan yang ditutupi oleh suatu bangun datar.
-
Rumus Luas Persegi:
Luas = sisi × sisi
Contoh Soal: Sebuah ubin berbentuk persegi memiliki panjang sisi 12 cm. Berapakah luas ubin tersebut?
Penyelesaian: Luas = 12 cm × 12 cm = 144 cm². -
Rumus Luas Persegi Panjang:
Luas = panjang × lebar
Contoh Soal: Sebuah meja belajar memiliki panjang 120 cm dan lebar 60 cm. Berapakah luas permukaan meja belajar tersebut?
Penyelesaian: Luas = 120 cm × 60 cm = 7200 cm². -
Rumus Luas Segitiga:
Luas = 1/2 × alas × tinggi
(Tinggi segitiga adalah garis tegak lurus dari salah satu sudut ke sisi di depannya atau perpanjangannya).
Contoh Soal: Sebuah segitiga memiliki alas 10 cm dan tinggi 8 cm. Hitunglah luas segitiga tersebut!
Penyelesaian: Luas = 1/2 × 10 cm × 8 cm = 40 cm². -
Rumus Luas Lingkaran:
Luas = π × jari-jari × jari-jari (r²)
(Menggunakan π = 3,14 atau 22/7)
Contoh Soal 1: Sebuah taman berbentuk lingkaran memiliki jari-jari 7 meter. Hitunglah luas taman tersebut menggunakan π = 22/7!
Penyelesaian: Luas = (22/7) × 7 meter × 7 meter = 22 × 7 meter² = 154 m².
Contoh Soal 2: Sebuah piringan hitam memiliki jari-jari 15 cm. Berapakah luas piringan hitam tersebut menggunakan π = 3,14!
Penyelesaian: Luas = 3,14 × 15 cm × 15 cm = 3,14 × 225 cm² = 706,5 cm². -
Soal Luas Gabungan Bangun Datar:
Sama seperti keliling, soal luas gabungan membutuhkan pemahaman untuk memecah bangun kompleks menjadi bangun-bangun sederhana yang luasnya dapat dihitung.
Contoh Soal: Sebuah lapangan berbentuk persegi panjang dengan ukuran 20 meter × 15 meter. Di salah satu sudut lapangan terdapat seperempat lingkaran dengan jari-jari 7 meter. Hitunglah luas lapangan yang tidak tertutup seperempat lingkaran tersebut!
Penyelesaian:- Hitung luas persegi panjang: Luas_PersegiPanjang = 20 m × 15 m = 300 m².
- Hitung luas seperempat lingkaran: Luas_Lingkaran = π × r² = (22/7) × 7 m × 7 m = 154 m². Luas_SeperempatLingkaran = 1/4 × 154 m² = 38,5 m².
- Luas lapangan yang tidak tertutup = Luas_PersegiPanjang – Luas_SeperempatLingkaran = 300 m² – 38,5 m² = 261,5 m².
5. Soal Cerita dan Penerapan dalam Kehidupan Nyata
Soal-soal bangun datar kelas 4 semester 2 seringkali disajikan dalam bentuk soal cerita. Tujuannya adalah agar siswa dapat mengaitkan konsep matematika dengan situasi sehari-hari. Kunci utama dalam menyelesaikan soal cerita adalah:
- Baca dengan Teliti: Pahami informasi apa saja yang diberikan dan apa yang ditanyakan.
- Identifikasi Bangun Datar: Tentukan bangun datar apa saja yang terlibat dalam cerita.
- Gambarkan (jika perlu): Membuat sketsa atau gambar sederhana dapat sangat membantu visualisasi masalah.
- Tentukan Rumus yang Tepat: Pilih rumus keliling atau luas yang sesuai dengan bangun datar dan pertanyaan yang diajukan.
- Lakukan Perhitungan: Hitung dengan cermat.
- Tulis Jawaban Lengkap: Sertakan satuan yang benar pada jawaban akhir.
Contoh Soal Cerita:
Pak Budi ingin memasang keramik pada lantai ruang tamu rumahnya yang berbentuk persegi panjang dengan ukuran 5 meter kali 4 meter. Harga keramik per meter perseginya adalah Rp 75.000. Berapa total biaya yang dibutuhkan Pak Budi untuk memasang keramik seluruh lantai ruang tamu tersebut?
Penyelesaian:
- Informasi: Ukuran ruang tamu (persegi panjang) 5 m × 4 m. Harga keramik Rp 75.000/m².
- Ditanya: Total biaya pemasangan keramik.
- Bangun Datar: Persegi panjang.
- Rumus: Luas persegi panjang (untuk mengetahui berapa meter persegi yang perlu ditutupi keramik).
Luas_RuangTamu = panjang × lebar = 5 m × 4 m = 20 m². - Perhitungan Biaya: Total Biaya = Luas_RuangTamu × Harga per m²
Total Biaya = 20 m² × Rp 75.000/m² = Rp 1.500.000. - Jawaban: Total biaya yang dibutuhkan Pak Budi adalah Rp 1.500.000.
6. Tips Tambahan untuk Menguasai Bangun Datar
- Latihan Rutin: Semakin banyak berlatih soal, semakin terbiasa siswa dengan berbagai tipe soal dan rumus.
- Pahami Konsep, Bukan Hafalan: Dorong siswa untuk memahami mengapa rumus tersebut berlaku, bukan hanya menghafalnya. Misalnya, luas persegi panjang adalah panjang kali lebar karena ia dapat disusun dari sejumlah persegi satuan sebanyak panjang dikali lebar.
- Gunakan Alat Peraga: Penggunaan penggaris, meteran, dan benda-benda berbentuk bangun datar dapat membantu visualisasi.
- Diskusi: Mengerjakan soal bersama teman atau bertanya kepada guru jika ada yang kurang dipahami sangat efektif.
- Fokus pada Satuan: Pastikan siswa selalu memperhatikan dan menuliskan satuan yang tepat (cm, m, cm², m²).
Penutup
Materi bangun datar kelas 4 semester 2 adalah tentang membangun pemahaman yang kuat tentang bentuk-bentuk di sekitar kita dan bagaimana mengukurnya. Dengan pemahaman yang baik tentang sifat-sifat, rumus keliling dan luas, serta latihan soal yang konsisten, siswa dapat dengan percaya diri menghadapi berbagai tantangan matematika yang berkaitan dengan bangun datar. Ingatlah bahwa matematika adalah sebuah petualangan, dan setiap soal yang terselesaikan adalah langkah maju dalam petualangan tersebut!